2 Lab #2: Energy and Heat Transfer
Lab #2: Energy and Radiation
Zachary J. Suriano
Introduction and Objectives
At its most basic, weather is a means of distributing energy within the atmosphere, moving or transferring energy from regions of surplus to regions of deficit. The main energy source for Earth is solar radiation, the primarily visible light received from the Sun. The amount of that radiation reaching the surface changes on a daily and seasonal basis due to the positioning of the Earth relative to the Sun, latitude, time of day, and atmospheric features such as cloud cover and atmospheric composition. In this lab, we will explore how energy is transferred within the Earth system and how the configuration of the Earth relative to the Sun and its energy results in our seasons.
Specific learning objectives of this lab are to:
- Differentiate processes that absorb and release latent heat
- Calculate how much and what type of radiation is emitted by objects of different temperatures
- Analyze and interpret graphics of shortwave and longwave radiation
- Determine where the Sun is directly overhead at solar noon for different days of the year
Latent Heat
Water exists in three phases within the Earth system as a liquid, solid, and gas and each plays a critical role in governing Earth’s energy balance. While we will explore these phases in future labs related to humidity, clouds, and precipitation, today we focus on the heat energy required to transition from one phase to the next: Latent Heat.
When water moves from its solid (ice) phase towards its gas (vapor) phase, latent heat is absorbed by the water from the surrounding environment. This can occur via melting, evaporation, and sublimation. We observe this as a decrease in the temperature of the air. Conversely, heat energy is released by the water to the surrounding environment during changes from vapor to ice phases. This occurs during condensation, freezing, and deposition. We observe this as an increase in the temperature of the air. The following table displays these processes and the amount of energy absorbed or released in units of calories per gram (cal/g).
| Latent Heat of: | Calories | Absorbed or Released by Water | Change in Temperature of Air | Process |
| Evaporation | 600 cal/g | Absorbed | Cooled | Liquid to water vapor |
| Condensation | 600 cal/g | Released | Warmed | Water vapor to water |
| Fusion | 80 cal/g | Absorbed | Cooled | Ice to liquid |
| Freezing | 80 cal/g | Released | Warmed | Liquid to ice |
| Sublimation | 680 cal/g | Absorbed | Cooled | Ice to water vapor |
| Deposition | 680 cal/g | Released | Warmed | Water vapor to ice |
Table 2-1. Energy absorbed or released during phase changes.
Concept Check #1:
During evaporation, latent heat is _____ by water resulting in a/an ______ in air temperature.
a. absorbed / decrease
b. absorbed / increase
c. released / decrease
d. released / increase
Radiation
As discussed in class, heat energy can be transferred four different ways: via Latent Heat, via Convection, via Conduction, and via Radiation. In this section, we will focus our attention on radiation, the transfer of heat energy through electromagnetic waves or as discrete packets of energy (photons). When considering radiation, there are three laws to keep in mind:
- All objects emit radiation as long as they have a temperature greater than absolute zero. This includes the Sun, the Earth, and us!
- Objects with higher temperatures emit more radiation. Mathematically, we represent this by the Stephan-Boltzmann equation (shown below)
- Objects with higher temperatures emit peak radiation in shorter wavelengths. Mathematically, this is represented by Wien’s Law equation (shown below).
Stephan-Boltzmann
E = (ε) x (σ) x (T4), Where E = energy emitted, ε = the emissivity of an object (or how effective of an absorber/emitter it is), σ = a constant, 5.67 x 10 -8 W/m2K4, and T4 = the temperature, raised to the 4th power, in units of K. For practical purposes in this class, we assume ε is equal to 1. This leaves σ and our temperature value to solve for how much energy is emitted by an object. An example problem is below, walking through each step.
Example Problem: How much energy is emitted by the Sun if we assume its temperature is 5900 K?
- Step 1: identify which equation to use. Here, we want to solve for energy emitted based on temperature, so we would need to use Stephan-Boltzmann.
- Step 2: write out the equation.
- o E = (ε) x (σ) x (T4)
- Step 3: plug in the known values for each term.
- o ε = 1 (no units)
- o σ = 5.67 x 10 -8 (units of W/m2K4)
- 5.67 x 10-8 = 0.0000000567
- o T = 5900 (units of K)
- o E = (1) x (5.67 x 10-8 W/m2K4) x (5900 K)4
- Step 4: Solve for T4
- o The exponent (4) indicates the temperature and its units should be multiplied by itself 4 times: 5900K x 5900K x 5900K x 5900K = (5900K)4 = 1.2117361 x 1015 K4 = 1,211,736,100,000,000 K4
- Step 5: Solve for entire equation
- o E = (1) x (5.67 x 10-8 W/m2K4) x (1,211,736,100,000,000 K4)
- o E = 68,705,436 W/m2
- o Note how when determining your units, σ has W / m2 K4, and you are multiplying by the units of T, K4. K4 / K4 cancel each other out, leaving W/m2.
Wien’s Law
λ = 2897 umK / T, Where λ is the wavelength of peak radiation emitted, 2897 umK is a constant, and T is the temperature in units K.
Example Problem: What the wavelength of peak energy emitted by the Sun if we assume its temperature is 5900K?
- Step 1: identify which equation to use. Here, we are solving for wavelength of peak energy, so we need Wien’s Law equation
- Step 2: write out the equation
- o λ = 2897 umK / T
- Step 3: plug in the known values for each term.
- o T = 5900K
- Step 4: Solve
- o λ = 2897 umK / T
- o λ = 2897 umK / 5900K
- o λ = 0.491 um
- units of um are micrometers, 10-6 meters.
Concept Check #2
Calculate the amount of energy emitted for an object with a temperature of 288.7 K. Round your final answer to 1 decimal place and includes the appropriate units.
Earth’s Energy Balance
If you were to calculate the wavelength of peak energy emitted by the Sun and by the Earth, you would see they are quite different. The Sun emits peak energy in the Visible wavelengths of the radiation spectrum. We call this energy shortwave radiation. Earth, conversely, emits peak energy in Infrared wavelengths. We call this energy longwave radiation. The Earth is constantly emitting longwave radiation, whereas it is only receiving shortwave radiation on locations of the planet that are facing the Sun (i.e., only during daylight hours is shortwave radiation being absorbed by the Earth). The ratio of how much energy is received at a location relative to how much energy is emitted is how the Energy Balance is calculated. Similar to a bank account, where you accumulate wealth when you receive more money than you spend, areas on the planet that receive more energy than they emit are considered to be areas of surplus. In the other direction, if you spend more money than you earn, you are depleting your wealth. For Earth’s energy balance, areas that emit more energy than they receive are in deficit.
We can view how much energy is being received at the surface by analyzing a graph of shortwave radiation at different times of the day, typically in units of W/m2. Below is an example from the Kentucky Mesonet weather station at the WKU Farm from February, 2023 (Figure 2-1).
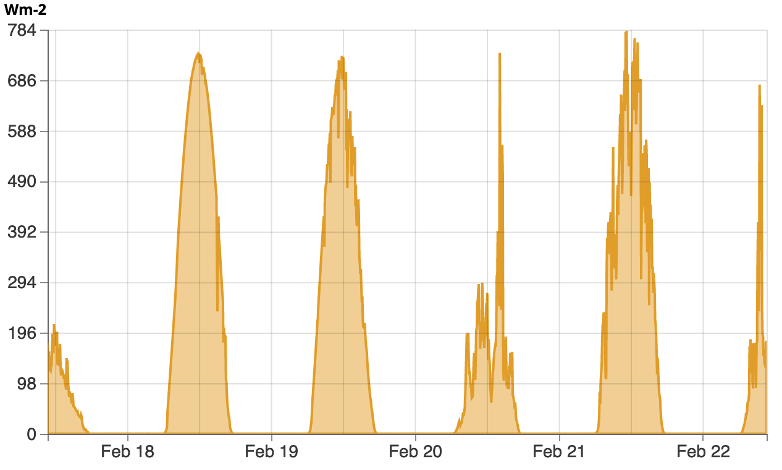
We notice how energy is only received during part of each day, corresponding to when we are in view of the Sun. Additionally, we notice how the amount of energy varies drastically during the course of some days, but is more uniform on others. This it often associated with varying cloud cover between individual days. When the skies are cloudy, part of the shortwave radiation is reflected and absorbed by the clouds reducing how much reaches the surface. In the case of Feb 20th, the day was mostly cloudy to start, but by mid-afternoon, breaks in the clouds allowed for large amounts of solar radiation to briefly reach the surface. To determine how much energy is received at a specific time, we find the intersection point where the amount of shortwave radiation received is at a specific time of day (below). So at 9am, the amount of energy was approximately 170 W/m2, while at 10am, it was approximately 190 W/m2.
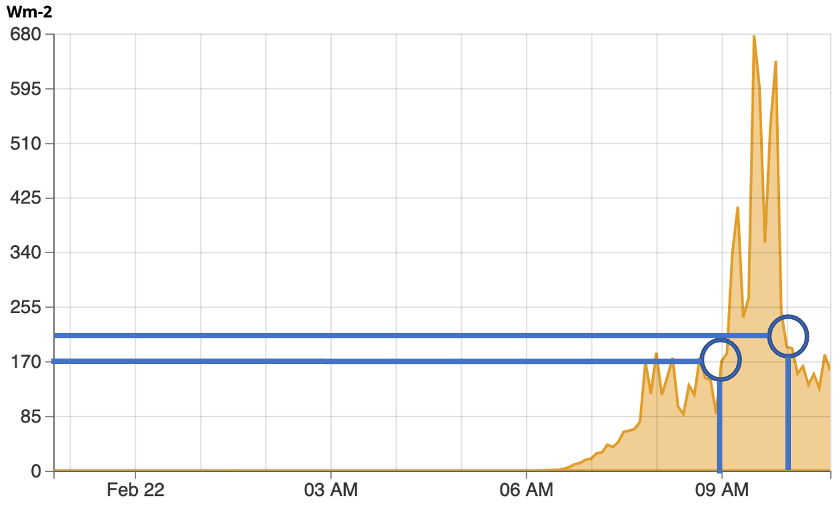
Concept Check #3
Using the provided graphic below, how much shortwave radiation was received at 3pm local time? Round your answer to the nearest whole degree and include “W/m2” in your answer.
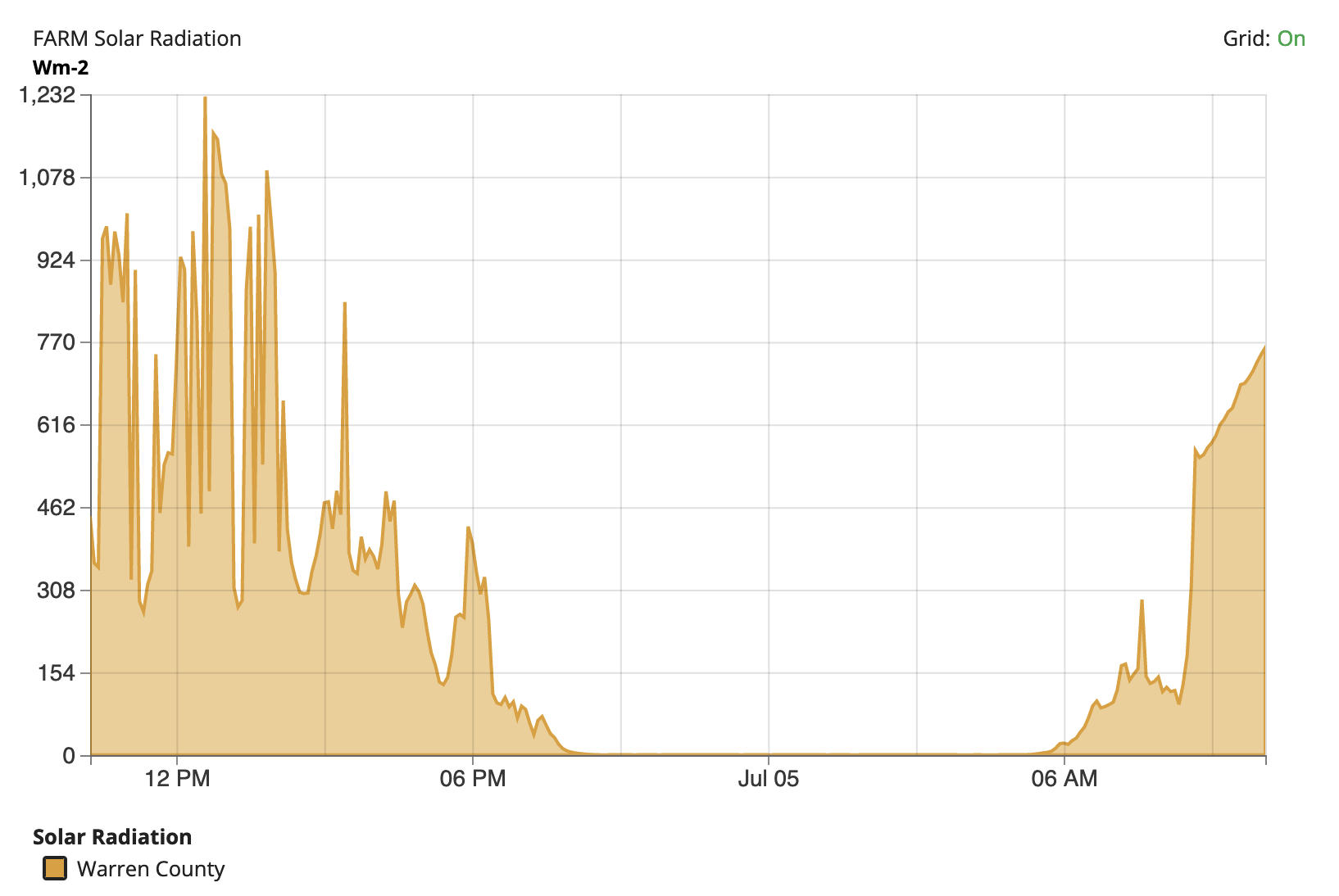
Earth’s Seasons
Because of Earth’s axial tilt, as we revolve around the Sun there are large changes in the amount short radiation incident on the surface of the planet for different latitudes. Three processes influence this amount of radiation and change throughout the calendar year: (1) the angle of the Sun’s energy incident on the surface, (2) the length of time the surface is receiving energy (i.e., day length), and (3) the amount of atmosphere the Sun’s energy needs to pass through to reach the surface.
When the angle of the Sun’s energy is large, or more directly overhead of a location, the amount of energy received is more concentrated per unit area. We know the Sun is directly overhead at solar noon during the Equinoxes and Solstices at specific latitudes, and can use this information to determine what the Sun angles are at other locations across the planet using the following equation: Sun Angle = 90 – |(latitude of location – latitude of where sun is directly overhead for a specific day)|. The latitude of location is expressed in degrees latitude, where locations in the Northern Hemisphere are positive, and locations in the Southern Hemisphere are negative. E.g., 40°N = 40, and 40°S = -40. The latitude of where the Sun is directly overhead will range from 23.5°N during the Summer Solstice, to 23.5°S (-23.5) during the Winter Solstice. During the two Equinoxes, the Sun is directly overhead at the equator, 0°. By taking the absolute value of the latitude differences, you can account for situations where the Sun is directly overhead in a different Hemisphere from your targeted location.
Practice Problem: What is the angle of the Sun at 37°N on the Summer Solstice?
- First Step is to write out the equation and our known values.
- o A = 90° – ( 37° – X )
- We next need to determine where the Sun is directly overhead at solar noon on the Summer Solstice. This is 23.5°N
- Plugging in: A = 90 – ( 37 – 23.5 )
- A = 90 – (13.5) A = 76.5°
- This is a relatively large value, indicating a relatively high concentration of energy received per unit area.
The longer the length of day, the more energy is received at that location. On the two Equinoxes, each location on the planet has 12 hours of daylight and 12 hours of darkness. On the Summer Solstice, locations in the Northern Hemisphere have longer days and shorter nights, while locations in the Southern Hemisphere have relatively shorter days and longer nights. On the Winter Solstice, we see the opposite where Northern Hemisphere locations have relatively shorter days and longer nights, and Southern Hemisphere locations have longer days and shorter nights. The table below provides approximate values of day length for locations by latitude.
| Latitude | Vernal/Autumnal Equinoxes (March/September) | Summer Solstice (June) | Winter Solstice (December) |
| 90°N | 12 hr | 24.0 hr | 0.0 hr |
| 60°N | 12 hr | 18.4 hr | 5.6 hr |
| 30°N | 12 hr | 13.9 hr | 10.1 hr |
| 0° | 12 hr | 12.0 hr | 12.0 hr |
| 30°S | 12 hr | 10.1 hr | 13.9 hr |
| 60°S | 12 hr | 5.6 hr | 18.4 hr |
| 90°S | 12 hr | 0.0 hr | 24.0 hr |
Table 2-2. Day length by latitude.
Finally, the amount of atmosphere the shortwave radiation needs to pass through to reach the surface and drastically change the amounts of scattering, reflection, and absorption that occur. When the Sun angle is low (i.e., close to the surface), the radiation needs to pass through much greater amounts of the atmosphere to reach the surface. This is because our atmosphere is compressible and most of the molecules, by mass, are located near the surface. When the Sun angle is low, the radiation passes through a greater layer of this near surface atmosphere where a larger percentage of the radiation is scattered, reflected, or absorbed by the atmosphere. For comparison, approximately 78% of shortwave radiation reaches the surface when the Sun is directly overhead (22% is lost) but when the Sun’s angle is at 30° of normal, only approximately 31% is received at the surface (69% is lost).
Concept Check #4
During the Spring (Vernal) Equinox, where is the Sun directly overhead at solar noon? What is the angle of the Sun’s energy at 37°N (i.e., Bowling Green)?